Калькулятор систем счисления

Система счисления — это символьный способ записи/представления чисел. В позиционной системе счислений значение каждого числового символа (цифры или буквы) в записи конечного числа зависит от его позиции, при этом количество цифр, необходимых для записи числа, называют основанием системы. Основание записывается справа от числа в нижнем индексе, например, 111011₂, 59₁₀, 3B₁₆.

Наиболее распространенными являются двоичная (программирование), десятичная (повсеместно), шестнадцатеричная (программирование) и шестидесятеричная системы (единицы измерения).

При помощи нашего калькулятора систем счисления можно выполнить конвертацию из одной системы в другую с подробным пошаговым решением. Программа осуществляет перевод целых и дробных положительных чисел, с отрицательными значениями конвертер не работает. Примеры пересчета представлены ниже, в таблице можно найти сопоставление чисел в десятеричной, двоичной и шестнадцатеричной системе.

Перевод числа из двоичной системы в десятичную — формула

q₁₀ = (a₁ × b^n-1) + (a₂ × b^n-2) + ... + (a_n × b^n-n)

a_1..n — цифра в двоичной системе на позиции от 1 до n;
b — основание двоичной системы;
n — количество символов в числе в двоичной системе;

Пример: 1010₂ = 10₁₀

q₁₀ = (1 × 2^4-1) + (0 × 2^4-2) + (1 × 2^4-3) + (0 × 2^4-4)
q₁₀ = 8 + 0 + 2 + 0 = 10₁₀

Перевод числа из десятичной системы в двоичную — формула

q₂ = i₁[a / b] i₂[p₁ / b] i₃[p₂ / b] ... i_n[p_n-1 / b]

a — число в десятичной системе;
b — основание двоичной системы;
i₁ — остаток от деления a на b;
i_2..n — остаток от деления p_1..n на b;
p₁ — результат деления a на b без остатка;
p_2..n — результат деления p_1..n на b без остатка.

*результат записывается в обратном порядке

Пример: 100₁₀ = 1100100₂

q₂ = 0[100/2] .. 0[50/2] .. 1[25/2] .. 0[12/2] .. 0[6/2] .. 1[3/2] .. 1[1/2]
q₂ = 1100100₂

Также расчет можно изобразить иным способом:

Перевод числа из десятичной системы в двоичную

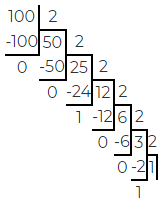
Таблица перевода чисел в системах счисления

Десятичная	Двоичная	Шестнадцатеричная
1	1	1
2	10	2
3	11	3
4	100	4
5	101	5
6	110	6
7	111	7
8	1000	8
9	1001	9
10	1010	A
11	1011	B
12	1100	C
13	1101	D
14	1110	E
15	1111	F
16	10000	10

Как перевести системы счисления?

Укажите исходную систему счисления.
Укажите конечную систему счисления.
Введите число, которое требуется перевести.
Нажмите кнопку «Рассчитать».

Смежные нормативные документы:

ГОСТ 8.417-2002 «Государственная система обеспечения единства измерений»
СТ СЭВ 543-77 «Числа. Правила записи и округления»